intro
写实验二的时候还是感觉头脑是一团浆糊, 归根结底还是B+tree操作不太熟悉, 还是不能跳过, 决定做一下hw2的B+Tree部分;
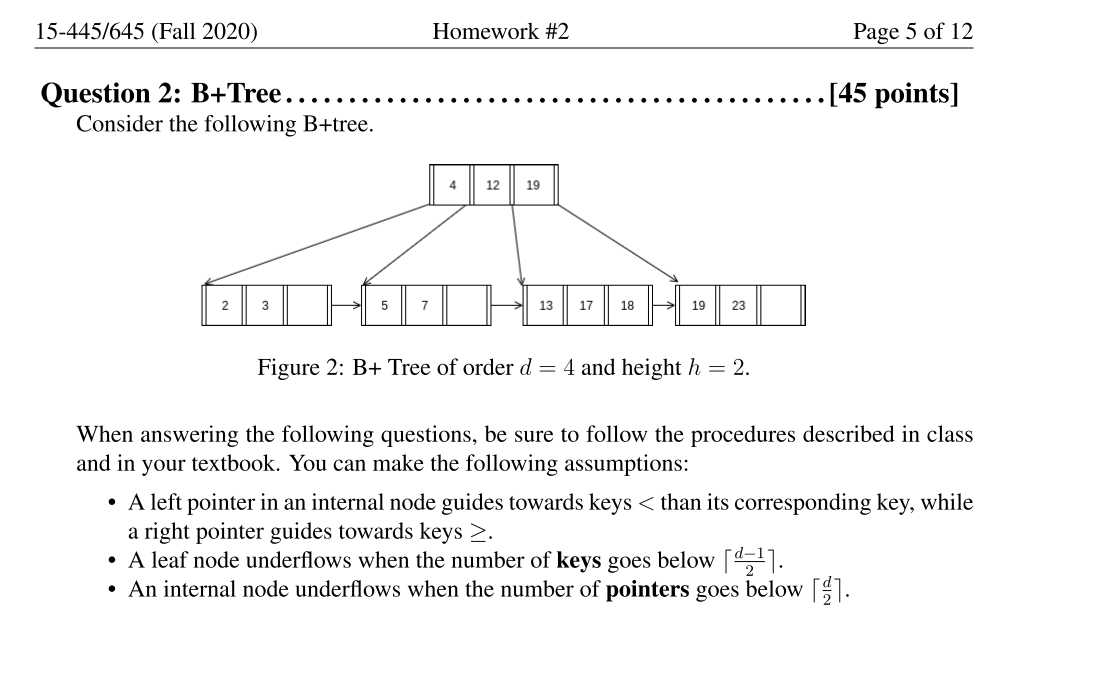
上图展现了我们要操作的b+tree的样子, 并且对B+Tree的结构做了简单的说明:
- 内部节点的左指针 指向了所有小于当前key的情况, 右指针指向了所有大于等于当前key的情况
- 叶子节点当关键字个数小于 d - 1 / 2向上取整的时候认为underflow, 在这个例子中d为4, 所以当#key小于2的时候发生下溢, 需要进行调整;
- 内部结点当指针数小于 d / 2向上取整的时候发生下溢, 这个例子中当指针数小于2的时候发生下溢, 需要调整
阅读数据库概念相关部分
插入部分
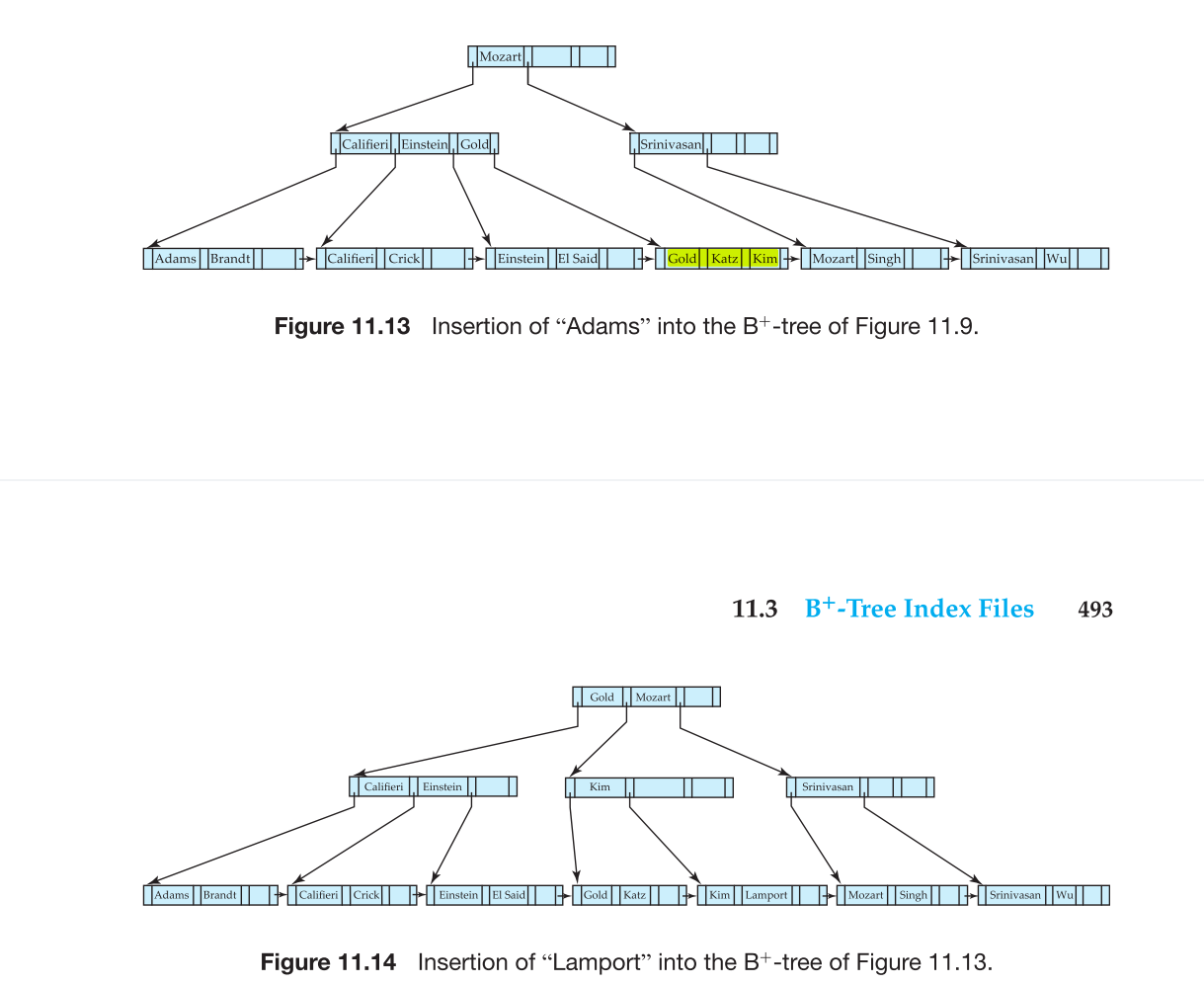
当要插入的结点(一定是叶子结点)满的时候需要进行分裂:
- 叶子结点有n个指针, n - 1个key, 所以插入后应该有n个key
- 将n /2向上取整个key留在原始结点, 剩下的结点放入新创建的结点中
- Having split a leaf node, we must insert the new leaf node into the B+-tree
structure - 新创建结点的第一个key肯定是这个结点中最小的key(所有结点内部都是按照key进行排序的), 所以我们应该把这个key 以及 指向这个新创建的结点的指针 组成的entry放入到parent结点中;
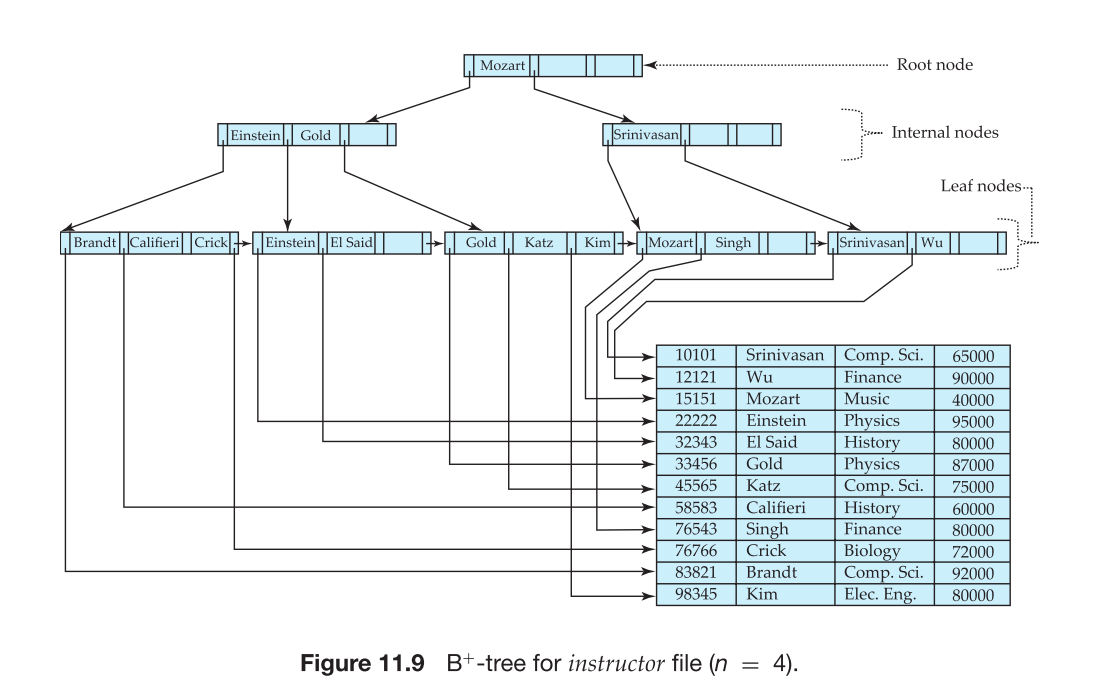
发现一个错误: 上图中应该是crick左指针指向76766
在上图中假设我们要插入Adam, 走路由, 按照 内部节点的左指针 指向了所有小于当前key的情况, 右指针指向了所有大于等于当前key的情况 这个规则, 我们可以顺利走到最左边的leaf node, 而这个结点是满的, n = 4, 应该把Adam, Brandt留在原始结点, Califieri, Crick放入新创建的结点; 这时候新节点的最小key也就是第一个key是Califieri, 我们将Califieri这个key, 以及指向这个新节点的指针放入parent node中, 而parent node中恰好有位置, 保持有序二分插入即可, 最后形成上一张截图中Figure 11.13的情况
然而并不是放入parent node中就能结束的, 有时候parent node也没有空间!!!
这种情况下, parent node也需要进行分裂, 但是内部结点的分裂和叶子结点的分裂是不同的!!!
To do so, the parent node is conceptually expanded temporarily, the entry added, and the overfull node is then immediately split.
However, the search key value that lies between the pointers that stay on the
left, and the pointers that move to the right node is treated differently. In our example, the search key value “Gold” lies between the three pointers that went to the left node, and the two pointers that went to the right node. The value “Gold” is not added to either of the split nodes. Instead, an entry (Gold, n2) is added to the parent node, where n2 is a pointer to the newly created node that resulted from the split. In this case, the parent node is the root, and it has enough space for the new entry.
不太好解释, 代码:


逐行瞎解释一下insert, 要插入的是一个key 和 一个 ptr, 这个ptr指向存放实际tuple的位置:
算了 不解释了, 先做…
第一题 下图插入14后结果长啥样?
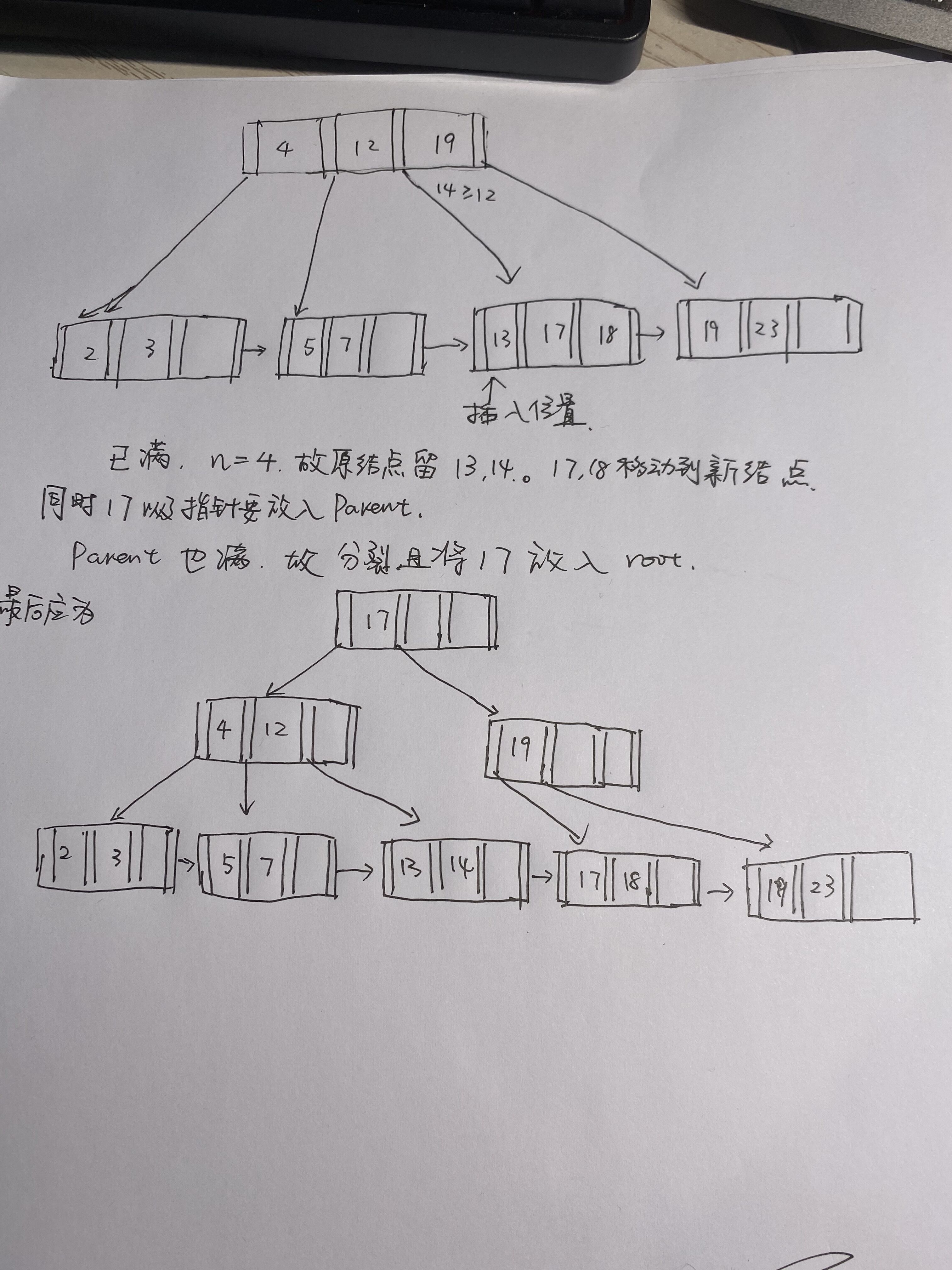
应该选c
第二题 How many pointers (parent-to-child and sibling-to-sibling) do you chase to find all keys between 5 and 15?
假设是在上一步基础上做的…
应该是4次吧(不知道需不需要走到17, 18 这个叶子节点再停止…)
删除


通过上面伪代码画红框的部分, 可以看到, 优先合并, 如果无法合并则再借结点.
删除方法简述如上, 在下图B+树上删除23

- 删除23, 叶子只剩一个key, underflow, 需要进行操作, 他的兄弟17, 18 结点还有一个位置, 可以进行合并, 将19以及指针拷贝进去, 将兄弟的 next_page指针(也就是最后一个指针)指向19这个结点的next, 也就是nullptr;
- 递归删除19这个父节点, 删掉key和ptr后剩一个指针, underflow, 兄弟4, 12这个结点还有位置, 需要进行合并, 这时候是内部节点, 所以将
K'(是父节点(root)中比N与N'之间的值, 这种情况下就是17), 以及当前这个结点中剩下的唯一一个指针(最左边的指针), 拷贝到4, 12中去; - 递归删除17这个root, 删掉17以及指针后, 当前结点是root而且只剩下
4, 12, 19这一个孩子, 那么将这个唯一的孩子设置为root, 并且将原来root结点删掉;
最后结果应该如下:
第三题 Finally insert 4∗ and delete 3∗. Select the resulting tree.
插入4:
4 >= 4, 所以走4的右指针进入第二个孩子, 这个孩子还有空间, 所以直接插入就行;
初步结果如下:
删除3:
删除3, 结点只剩下一个key, underflow, 兄弟没有位置, 无法进行合并, 所以要进行redistribution(借结点):
redistribution 伪代码:

N'不是N的predecessor, 所以走symmetric:
N是leaf node, 走对称的else:
将4, 5, 7这个结点的第一个key 和 ptr插入到2这个结点的末尾, 再将剩下的5, 7的第一个key 5 , 替换parent中的4;
所以最后结果如下:
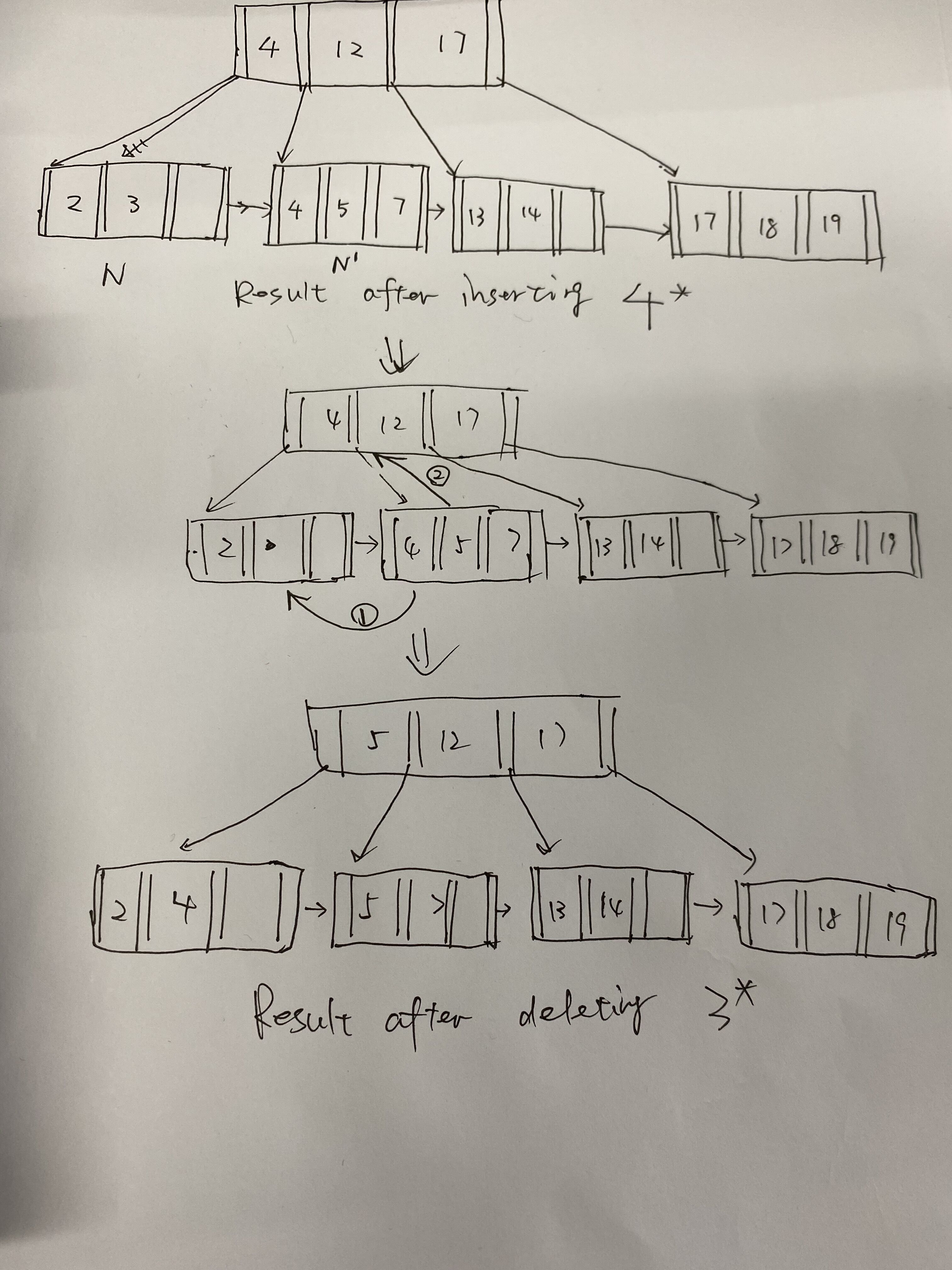
应该选A;