算法导论复习

misc

拿了字节offer好开心. 10号考算法, 复习加水一篇博客. 希望不要被八强啊;

注: 以下代码都是直接再typora上敲的, 不保证其正确性

引言

什么是算法及其特征

算法是通过一个有限的指令序列集合对特定的问题进行求解的一种计算执行描述。

（1）输入：一个算法具有零个或多个取自指定集合的 输入值；

（2）输出：对算法的每一次输入，算法具有一个或多个与输入值相联系的输出值

（3）确定性：算法的每一个指令步骤都是明确的；

（4）有限性：对算法的每一次输入，算法都必须在有 限步骤（即有限时间）内结束；

（5）正确性：对每一次输入，算法应产生出正确的输 出值；

（6）通用性：算法的执行过程可应用于所有同类求解 问题，而不是仅适用于特殊的输入。

问题实例和问题规模

问题实例是计算问题的解决方案所需的全部输入

问题规模是算法的输入实例大小。

算法初步

插入排序算法

loop invariant: 当前指针左边数组已排序

1
2
3
4
5
6
7
8
9
10
11
12
void insertionSort(vector<int> &nums) {
    int n = nums.size();
    if (n < 2) return;
    for (int i = 1; i < n; ++i) {
        int num = nums[i];
        int j = i - 1;
        for ( ; j >= 0 && nums[j] > num; --j) {
            nums[j + 1] = nums[j];
        }
        nums[j] = num;
    }
}

分析: 整体复杂度显然为一个三角形, 面积为O(n^2), 对于基本有序的输入友好(O(n), 因为j指针动不了);

最坏O(n^2)、最好O(n^2)和平均O(n)情形复杂性

归并排序算法

可以用来计算逆序对;

归并的基本思想是分治, 而分治思想主要分为三个部分:

  • divide - 归并中的取中间下标
  • conquer- 递归调用
  • combine -两个有序子数组的merge

同样使用分治思想的还有快速排序(combine过程无需做), 平面上找最近点对.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
void merge(vector<int> &nums, int lo, int mid, int hi) {
    // aux arr
   	int n1 = mid - lo + 1; //闭区间
    int n2 = hi - mid; // 左开右闭
   	vector<int> left(n1 + 1), right(n2 + 1); // 多申请一个空间作为哨兵
    // copy elem to aux arr
    for (int i = 0; i < n1; ++i) {
        left[i] = nums[i + lo];
    }
    left[n1] = INT_MAX;
    for (int i = 0; i < n2; ++i) {
        right[i] = nums[mid + 1 + i];
    }
    right[n2] = INT_MAX;
    // merge
    int i = 0, j = 0;
    for (int idx = lo; idx <= hi; ++idx) {
        if (left[i] <= right[j]) {
            nums[idx] = left[i++];
        }
        else {
            nums[idx] = right[j++];
        }
    }
}

void mergeSort(vector<int> &nums, int lo, int hi) {
    if (lo < hi) {
        int mid = lo + hi >> 1;
        mergeSort(nums, lo, mid);
        mergeSort(nums, mid + 1, hi);
        merge(nums, lo, mid, hi);
    }
}

时间复杂度为O(nlogn), 空间复杂度为: 递归栈logn, 辅助数组总长度On, 故为O(n)

常见排序算法复杂度:

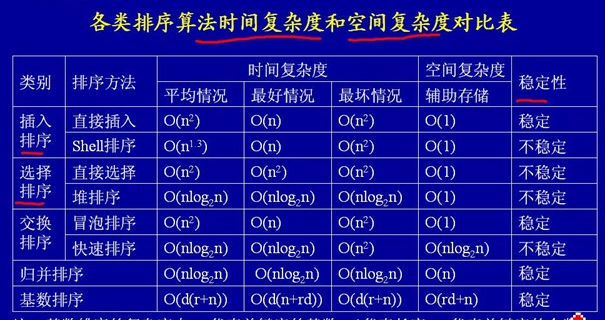
堆排序

堆的逻辑结构是完全二叉树, 实际存储结构是数组

对于一个结点i, 其父亲为i/2, 左孩子为2 * i + 1, 右孩子为2 * i + 2;

堆主要核心的代码就是swim 和 sink, 具体就不写了.

中位数和顺序统计

最大最小值

单独求一个无序数组的最值, 比较次数显然为n - 1, 代码如下:

1
2
3
4
5
6
7
8
9
int maxVal(vector<int> &nums) {
    int res = nums[0];
    for (int i = 1; i < nums.size(); ++i) {
        if (nums[i] > res) {
            res = nums[i];
        }
    }
    return res;
}

同时求最大最小值:

  • 分别求: 则比较次数为 n - 1 + n - 2 = 2n - 3;
  • 同时求显然可以减少比较次数, 循环执行了 n / 2次, 每次循环内3次比较, 所以只比较了3n / 2次;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
vector<int> minAndMax(vector<int> &nums) {
	int n = nums.size();
    int maxVal = INT_MIN, minVal = INT_MAX;
    for (int i = 1; i < n; i += 2) {
        int num1 = nums[i - 1];
        int num2 = nums[i];
        if (num1 > num2) {  // 保证num1 < num2, 第一次比较
            swap(num1, num2);
        }
        minVal = min(minVal, num1); // 第二次比较
        maxVal = max(maxVal, num2); // 第三次比较
    }
    if (i == n) { // 说明最后一个元素尚未比较
        int num = nums[n - 1];
        minVal = min(minVal, num);
        maxVal = max(maxVal, num);
    }
    return {minVal, maxVal};
}

topk问题: 期望时间为线性的选择

选出无序序列中第k大 或者 前k大个数字的时候 一定 一定使用这种方法(能放入内存的情况下)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
int topk(vector<int> &nums, int lo, int hi, int k) {
    if (k > nums.size()) return -1;
    if (lo == hi) return nums[lo];
    if (lo < hi) {
        int q = partition(nums, lo, hi);
        if (q == k) return nums[q];
        else if (q < k) {
            return topk(nums, q + 1, hi, k);
        }
        else {
            return topk(nums, lo, q - 1, k);
        }
    }
}

int partition(vector<int> &nums, int lo, int hi) {
    int pivot = nums[hi];
    int i = lo;
    for (int j = lo; j < hi; ++j) {
        if (nums[j] <= pivot) {
            swap(nums[i++], nums[j]);
        }
    }
    swap(nums[i], nums[hi]);
    return i;
}

时间复杂度O(n)

topk问题: 最坏时间为线性的选择

这算法有点难, 一般面试也不会用上, 随便看看吧

红黑树

红黑树是一种放宽了限制的avl树(通过引入红节点), 所以查询性能比avl树弱, 但是插入删除旋转次数较少, 它有如下五个基本性质:

  • 每个结点红或者黑
  • 根为黑
  • nil结点为黑
  • 若节点为红, 则两个孩子必为黑(即没有两个红节点直接连接)
  • 每个结点到所有后代叶子的路径有同样多的黑结点(黑高相等)

一棵n个内点的红黑树的高度至多 是2log(n+1)。

插入算法的时间、至多使用2次旋转

删除算法的时间、至多使用3次旋转

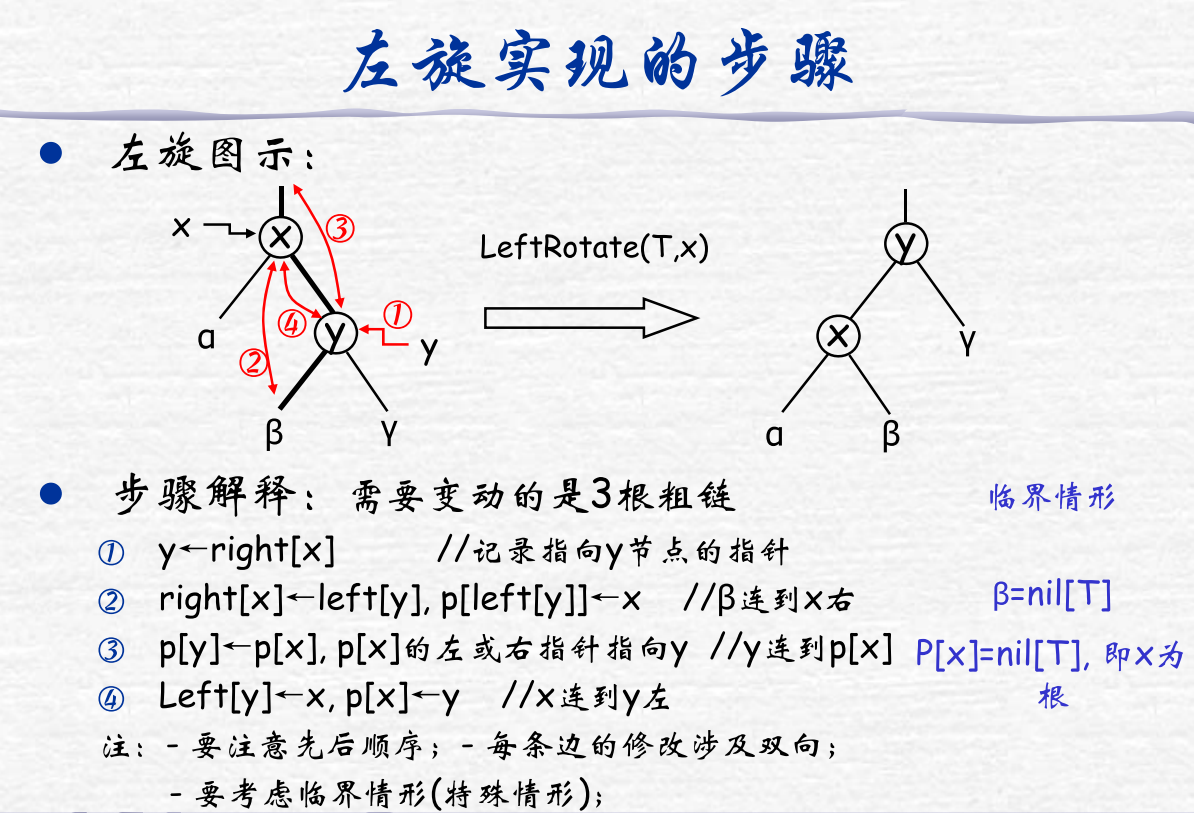
红黑树左旋

红黑树插入

step 1：将z节点按BST树规则插入红黑树中， z是叶子节点；

step 2：将z涂红；

step 3：调整使其满足红黑树的性质；

OS树

os树就是红黑树维护了size属性;

OS-select(x, i): 选择以x为根的子树中, 查找第i个最小元素

1
2
3
4
5
6
7
8
9
10
TreeNode *OSSelect(TreeNode *x, int i) {
    int rank = x->left->size + 1;
    if (rank == i) return x;
    else if (i < rank) {
        return OSSelect(x->left, i);
    }
    else {
        return OSSelect(x->right, i - rank);
    }
}

OSRank(TreeNode *x): 在以x为根的自述中求x的秩:

不相交集合的数据结构

主要是并查集, 主要用来计算连通分量个数, 计算朋友圈…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class UF {
public: 
    UF(int n) { // init a uf with n nodes
        p.resize(n);
        for (int i = 0; i < n; ++i) {
            p[i] = i;
        }
        setCount = n;
    }
    
    int find(int x) { // find with path compression
        return x == p[x] ? x : p[x] = find(p[x]);
    }
    
    void connect(int x, int y) {
        int f1 = find(x), f2 = find(y);
        if (f1 != f2) {
            --setCount;
            p[f1] = f2;
        }
    }
    
    
    vector<int> p; // parent
    int setCount; // # of sets
};

图论

BFS和DFS算法

  • 白色、灰色和黑色结点概念和作用
    • 所有节点一开始被初始化为白色, 颜色属性保存再结点color域中
    • 所有与黑色结点邻接的结点都已经被发现
    • 灰色结点是代表的是已访问和未访问两个集合的边界
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
enum {white = 0, gray = 1, black = 2};
struct Node {
    int color;
    int dist;
    Node *pre;
};

void bfs(graph g, Node *s) {  // g代表整张图, s为bfs搜索起始节点
    // 初始化其余节点信息
    for (Node *node : g.vertices - s) { // 半伪代码
        node->color = white;
        node->dist = INT_MAX;
        node->pre = nullptr;
    }
    s->color = gray; // 因为gray代表的是已知和未知两个集合之间的边界
    s->dist = 0;
    s->pre = nullptr;
    queue<Node *> q;
    q.push(s);
    while (q.size()) {
        Node *u = q.front();
        q.pop();
        for (Node *v : u->adj()) { // 假设adj能够返回邻接的结点指针
            if (v->color == white) { // v尚未被访问过
                v->color = gray;
                q.push(v);
                v->dist = u->dist + 1;
                v->pre = u;
            }
        }
        u->color = black; // 至此, u之和黑色或者灰色结点邻接
    }
}

  • 计算过程及其时间复杂度
赏

谢谢你请我吃糖果

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

很惭愧<br><br>只做了一点微小的工作<br>谢谢大家