3 TechLead problems:trie, topk and memorized

2021-01-22

motivation

Top “Hard” Interview Problems from Google, Facebook, FANG (for software engineers) - YouTube

看了这个视频, 视频中解决了三个问题, 刚好这三个问题都比较经典, 所以记录一下.

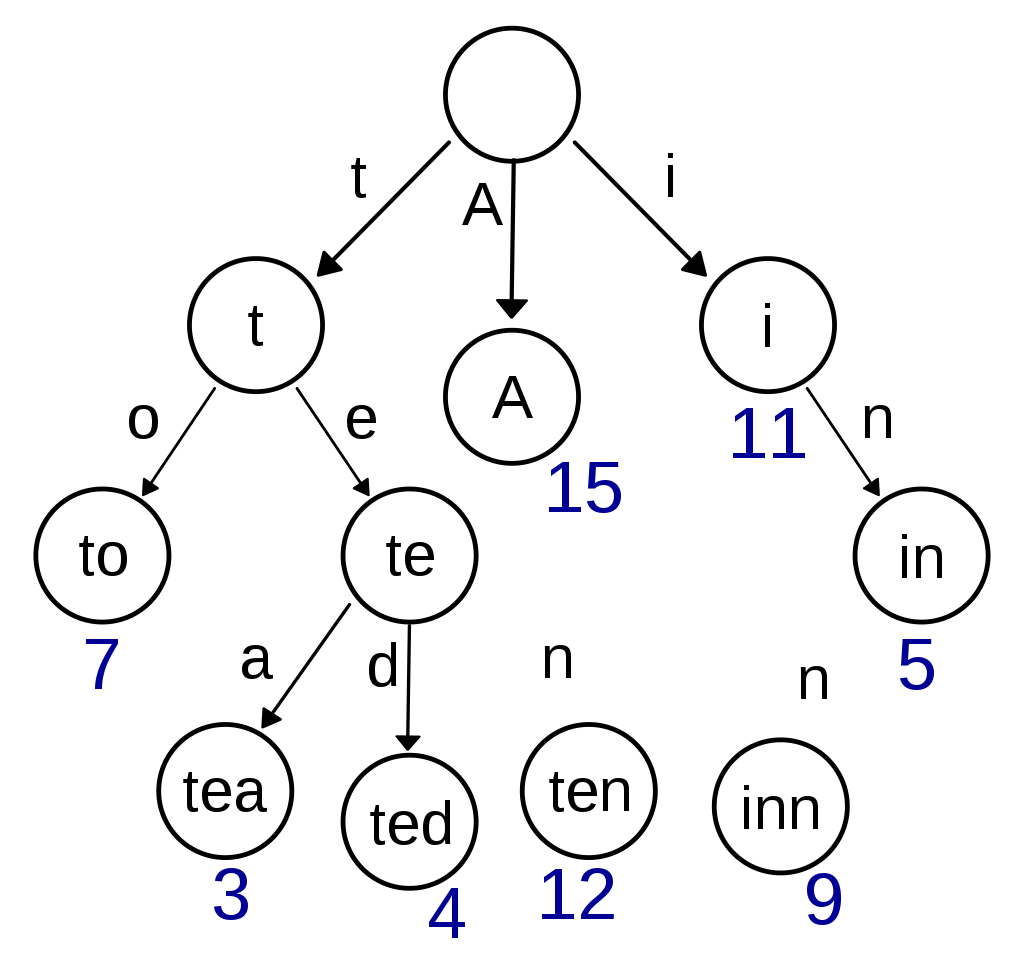
1 trie的应用:

问题:
- “You are given a prefix and a list of words, you need to return all the potential words that would match this prefix”
- eg: prefix "do" , word-list:["dog", "dark", "cat", "door", "dodge"], the potential words would be ["dog", "door", "dodge"];

分析:

假设prefix长度为k, word-list长度为n
brutal force:
- 遍历word-list中每一个单词, 检查每个单词的前k为是否和prefix相同, 是则加入res
- 时间复杂度O(nk)
代码:

class Solution {
public:
    vector<string> brutal(vector<string> &words, string &prefix) {
        vector<string> res;
        int k = prefix.size();
        for (string word : words) {
            if (word.size() < k) continue;
            bool flag = true;
            for (int i = 0; i < k; ++i) {
                if (word[i] != prefix[i]) {
                    flag = false;
                    break;
                }
            }
            if (flag) res.push_back(word);
        }
        return res;
    }
};


int main() {
    vector<string> words{"dog", "dark", "cat", "door", "dodge"};
    string prefix {"do"};
    Solution solution;
    auto res = solution.brutal(words, prefix);
    for (auto &x : res) {
        cout << x << " ";
    }
    return 0;
}

使用Trie (时间复杂度为O(k) + O(n), 所有单词可能都在这个子树下)

代码

#include <vector>
#include <string>
#include <iostream>
using namespace std;

struct Node {  // trie 结点定义
    Node *children[26];
    bool isWord;
    Node() {
        for (auto & i : children) {
            i = nullptr;
        }
        isWord = false;
    }
};


class Solution {
public:
    Node *trie;
    Solution() {  // 构造一个空结点
        trie = new Node;
    }

    void build(vector<string> &words) {
        for (string &word : words) {
            Node *cur = trie;
            for (char c : word) {
                if (!cur->children[c - 'a']) { // 对应孩子没有路径
                    Node *node = new Node;
                    node->isWord = false;
                    cur->children[c - 'a'] = node;
                }
                cur = cur->children[c - 'a'];
            }
            cur->isWord = true;
        }
    }

    vector<string> ansWithTrie(vector<string> &words, string &prefix) {
        build(words);
        vector<string> res;
        Node *cur = trie;
        for (char c : prefix) {  // 走到对应子树的根
            if (!cur->children[c - 'a']) return res;
            cur = cur->children[c - 'a'];
        }
        dfs(cur, res,  prefix);
        return res;
    }

    void dfs(Node *cur, vector<string> &res, string tmp) {
        if (!cur) return;
        if (cur->isWord) res.push_back(tmp);
        for (int i = 0; i < 26; ++i) {
            if (cur->children[i]) {
                char c = 'a' + i;
                dfs(cur->children[i], res, tmp + c);
            }
        }
    }
};


int main() {
    vector<string> words{"dog", "dark", "cat", "door", "dodge"};
    string prefix {"do"};
    Solution solution;
    auto res = solution.ansWithTrie(words, prefix);
    for (auto &x : res) {
        cout << x << " ";
    }
    return 0;
}

- 以上代码针对26个小写字母, 如果全部要支持, 扩展到256ascii码即可.

2 TopK

问题
- 给一个未排序的数组, 返回第k大的元素
分析:
- 方法1, 每次拿最大的, 并且vis标记该结点已经访问过, 拿K次, 时间复杂度O(nk), 空间O(n);
- 方法2, sort, 返回下标为size - k的位置的值, 时间复杂度O(nlogn), 空间快排空间, 可认为是O(1);
- 方法3, 使用heap, 拿k次最大值. 建堆O(n), extract-max O(logn), 所以总时间复杂度为O(n + klogn);
- 最佳方法:基于partition (算法导论版本最好, 不要改了!!!), 递推式近似为T(n) = T(n/2) + n, 时间复杂度显然为n + n/2 + n/4 + n/8 +… = 2n = O(n);
代码:

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

class Solution {
public:
    int ans1(vector<int> &nums, int k) {
        int n = nums.size();
        if (n < k) return -1;
        vector<bool> vis(n, false);
        int idx = -1;
        for (int i = 0; i < k; ++i) {
            idx = -1;
            for (int j = 0; j < n; ++j) {
                if (!vis[j] && (idx == - 1 || nums[idx] < nums[j])) {
                    idx = j;
                }
            }
            vis[idx] = true;
        }
        return nums[idx];
    }

    int partition(vector<int> &nums, int lo, int hi) {
        int pivot = nums[hi];
        int i = lo;
        for (int j = lo; j < hi; ++j) {
            if (nums[j] < pivot) {
                swap(nums[i], nums[j]);
                ++i;
            }
        }
        swap(nums[i], nums[hi]);
        return i;
    }

    int topK(vector<int> &nums, int k) {
        int n = nums.size();
        int lo = 0, hi = n - 1;
        while (lo <= hi) {
            int q = partition(nums, lo, hi);
            if (q == n - k) {
                return nums[q];
            }
            else if (q > n - k) {
                hi = q - 1;
            }
            else lo = q + 1;
        }
        return -1;
    }
};

int main () {
    Solution solution;
    vector<int> nums{5, 7, 2, 3, 4, 1, 6};
    cout << solution.ans1(nums, 3) << endl;
    cout << solution.topK(nums, 3) << endl;
    return 0;
}

3 单词组合

问题
- 给定一些words, 判断哪些word 可以由别的word组合(concatenate)而成, 返回所有这些可以被别人组合而成的word
- 例如: words:{“cat”, “cats”, “dog”, “catsdog”}, 我们应该返回{“catdogs”}, 因为只有”catsdog”可以由别的单词(“cats” + “dog”) 组合而成.
分析
- 对于每一个单词, 例如”catsdog” , 可以拆分为两部分, 第一部分直接查询unordered_set观察是否存在, 如果存在, 则递归第二部分. 例如:
  - 拆分为”c” , “atsdog”, “c”在words set里面不存, 返回
  - 拆分为”ca” , “tsdog”, “ca”不存在, 返回
  - 拆分为”cat”, “sdog”, “cat” 存在, 递归”sdog”, 返回false, 故总体不存在
  - 拆分为”cats”, “dog”, “cats”存在, 递归”dog”, 下面展示递归”dog”的过程:
    - 拆为 “d”, “og”, “d”不存在, 返回
    - 拆为”do”, “g”, “do”不存在, 返回
    - 拆为”dog”, “”, “dog”存在, 递归””, 对于空字符串, 递归返回true, 故整体返回true.
  - 故整体”catsdog”可以是别的word的concatenation, 加入res中.
暴力复杂度分析
- 假设words.size 为n, 每个word平均长度为m, O(n * 2 ^m), 具体怎么分析没弄懂
优化
- 可以使用cache来保存哪些满足条件的word(不管是不是一个subword), 使得时间复杂度降低到(n * m^2);
代码:

class Solution1 {
public:
    unordered_set<string> wordsSet;
    unordered_set<string> cache;
    vector<string> getConcatenatedWords(vector<string> &words) {
        vector<string> res;
        for (const string &word : words) {
            wordsSet.insert(word);
        }
        for (string &word : words) {
            if (isConcatenated(word)) {
                res.push_back(word);
            }
        }
        return res;
    }

    bool isConcatenated(string &word) {
        if (word.empty()) return true;
        if (cache.count(word)) return true;
        int n = word.size();
        for (int subLen = 1; subLen < n; ++subLen) {
            string part1 = word.substr(0, subLen);
            if (wordsSet.count(part1)) {
                string part2 = word.substr(subLen);
                if (wordsSet.count(part2) or isConcatenated(part2)) {
                    // cache
                    cache.insert(word);
                    return true;
                }
            }
        }
        return false;
    }

};


int main () {
    Solution1 solution1;
    vector<string> words{"cat", "cats", "dog", "catsdog"};
    auto res = solution1.getConcatenatedWords(words);
    for (const auto &word : res) {
        cout << word << endl;
    }
    return 0;
}

总结

测试驱动编程, 可以先把如何调用这个函数(类)写好, 再写具体代码
每个函数可以先把函数签名和返回值准备好
记忆化搜索, 大大降低时间复杂度
trie C++实现一般需要写构造函数, 明确地将children指针都置为nullptr
trie不需要显示得存储char, 因为char的信息已经被隐式得存储在下标之中